Higher-order geometry differences and intersections

st_intersection
st_difference
Further reading

Suppose you have the following geometry, consisting of three overlapping square polygons:

library(sf)

## Loading required package: methods

## Linking to GEOS 3.5.1, GDAL 2.1.2, proj.4 4.9.3

pol = st_polygon(list(rbind(c(0,0), c(1,0), c(1,1), c(0,1), c(0,0))))
b = st_sfc(pol, pol + c(.8, .2), pol + c(.2, .8))
par(mar = rep(0, 4))
plot(b, col = NA)

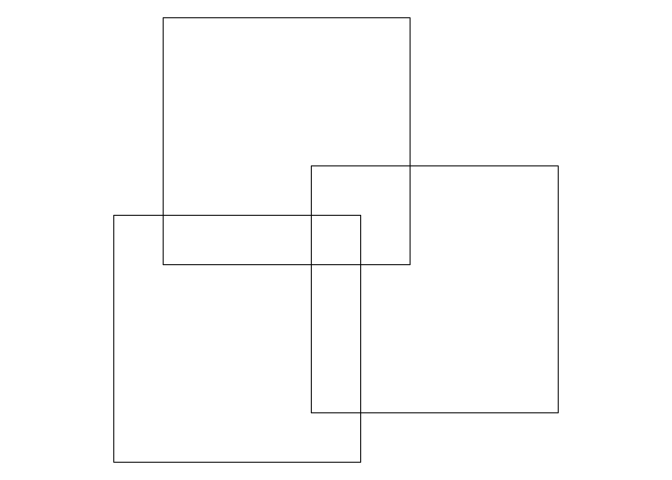
and you are interested in the area where all squares overlap (green), or where exactly two squares overlap (orange):

i = st_intersection(st_sf(b))
par(mar = rep(0, 4))
cl = sf.colors(3, categorical = TRUE)
plot(b)
plot(i[i$n.overlaps == 3,2], col = cl[1], add = TRUE)
plot(i[i$n.overlaps == 2,2], col = cl[2], add = TRUE)

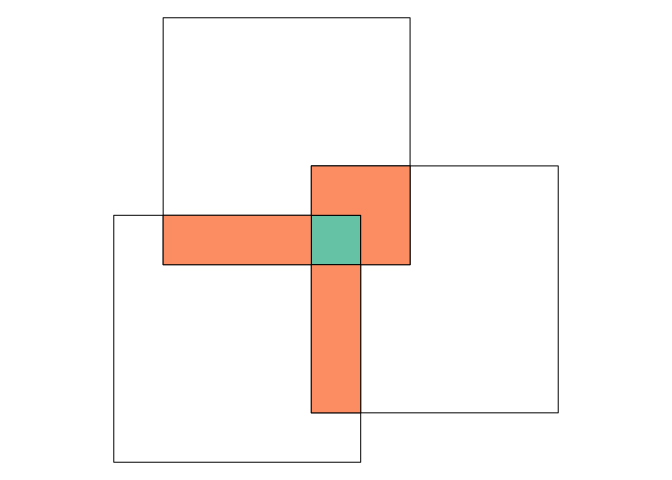
So far, with package sf or rgeos you could only get pairwise intersections, meaning you would have to go through all pairwise intersections and see whether they are intersected by others geometries or intersections. In this StackOverflow question you can get an idea how ugly this can get.

st_intersection

Now, inspired by a meticulously prepared pull request by Jeffrey Hanson, it suffices to do

(i = st_intersection(b))

## Geometry set for 7 features 
## geometry type:  POLYGON
## dimension:      XY
## bbox:           xmin: 0 ymin: 0 xmax: 1.8 ymax: 1.8
## epsg (SRID):    NA
## proj4string:    NA
## First 5 geometries:

## POLYGON ((1 0.2, 1 0, 0 0, 0 1, 0.2 1, 0.2 0.8,...

## POLYGON ((1 0.8, 1 0.2, 0.8 0.2, 0.8 0.8, 1 0.8))

## POLYGON ((1.2 1.2, 1.8 1.2, 1.8 0.2, 1 0.2, 1 0...

## POLYGON ((0.2 1, 0.8 1, 0.8 0.8, 0.2 0.8, 0.2 1))

## POLYGON ((0.8 1, 1 1, 1 0.8, 0.8 0.8, 0.8 1))

to get all the unique pieces, for each unique piece the number of contributing geometries, and a list-column with indexes of the geometries that contribute (overlap) for a particular piece.

st_difference

The pull request Jeffrey wrote was to remove (erase) all overlapping pieces, which you now get by

d = st_difference(b)
plot(d, col = cl)

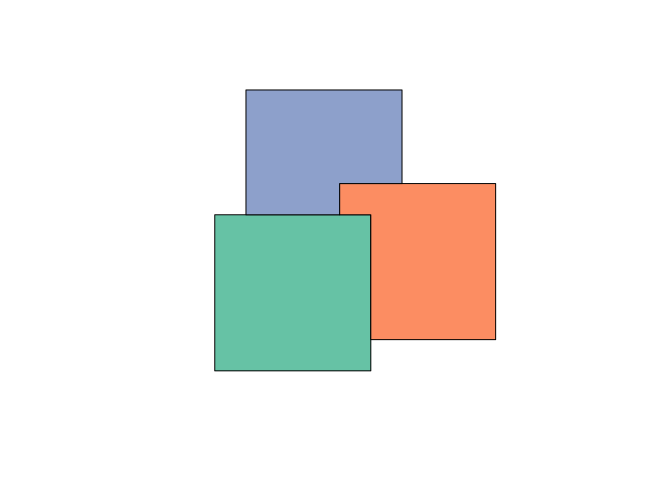
For this latter approach, obviously the input order matters: what is returned are non-empty geometries with \(x_1\), \(x_2 - x_1\), \(x_3 - x_2 - x_1\) etc.

To prove that these intersections or differences do not have any overlaps, we can compute overlaps by

st_overlaps(i)

## Sparse geometry binary predicate list of length 7, where the predicate was `overlaps'
##  1: (empty)
##  2: (empty)
##  3: (empty)
##  4: (empty)
##  5: (empty)
##  6: (empty)
##  7: (empty)

st_overlaps(d)

## Sparse geometry binary predicate list of length 3, where the predicate was `overlaps'
##  1: (empty)
##  2: (empty)
##  3: (empty)

st_intersection

st_difference

Further reading